XAT 2015 Quant & DI

Quantitative Reasoning and Data Interpretation section in XAT 2015 had 31 questions. Detailed explanation and video solution to questions have been provided.

1. What is the sum of the following series?   -64, -66, -68, ..... , -100

   1. -1458
   2. -1558
   3. -1568
   4. -1664
   5. None of the above

   • Choice BThe sum of the sequence is -1558. Correct answer
   • Explanatory answer
   • Arithmetic Progression
   • Easy
   • Video Explanation

2. The Maximum Retail Price (MRP) of a product is 55% above its manufacturing cost. The product is sold through a retailer, who earns 23% profit on his purchase price. What is the profit percentage (expressed in nearest integer) for the manufacturer who sells his product to the retailer? The retailer gives 10% discount on MRP.

   1. 31%
   2. 22%
   3. 15%
   4. 13%
   5. 11%

   • Choice DThe profit made by the manufacturer is 13% Correct answer
   • Explanatory answer
   • Profit & Loss
   • Medium
   • Video Solution

3. Ramesh plans to order a birthday gift for his friend from an online retailer. However, the birthday coincides with the festival season during which there is a huge demand for buying online goods and hence deliveries are often delayed. He estimates that the probability of receiving the gift, in time, from the retailers A, B, C and D would be 0.6, 0.8, 0.9 and 0.5 respectively. Playing safe, he orders from all four retailers simultaneously. What would be the probability that his friend would receive the gift in time?

   1. 0.004
   2. 0.006
   3. 0.216
   4. 0.994
   5. 0.996

   • Choice EThe probability that Ramesh's friend will receive the gift is 0.996 Correct answer
   • Explanatory answer
   • Probability
   • Medium
   • Video Explanation

4. The figure below has been obtained by folding a rectangle. The total area of the figure (as visible) is 144 square meters. Had the rectangle not been folded, the current overlapping part would have been a square. What would have been the total area of the original unfolded rectangle?

   

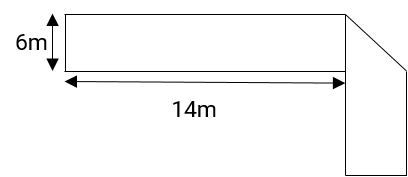
   1. 128 square meters
   2. 154 square meters
   3. 162 square meters
   4. 172 square meters
   5. None of the above

   • Choice CThe area of the unfolded rectangle is 162 sq m Correct answer
   • Explanatory answer
   • Mensuration
   • Medium
   • Video Solution

5. A solid metal cylinder of 10 cm height and 14 cm diameter is melted and re-cast into two cones in the proportion of 3 : 4 (volume), keeping the height 10 cm. What would be the percentage change in the flat surface area before and after?

   1. 9%
   2. 16%
   3. 25%
   4. 50%
   5. None of the above

   • Choice DThe flat surace area increases by 50% Correct answer
   • Explanatory answer
   • Mensuration : Solid Geometry
   • Medium
   • Video Explanation

6. A circular road is constructed outside a square field. The perimeter of the square field is 200 ft. If the width of the road is 7√2 ft. and cost of construction is Rs. 100 per sq. ft. Find the lowest possible cost to construct 50% of the total road.

   1. Rs.70,400
   2. Rs.1,25,400
   3. Rs.1,40,800
   4. Rs.2,35,400
   5. None of the above

   • Choice BThe lowest cost of constructing 50% of the road is Rs.1,25,400 Correct answer
   • Explanatory answer
   • Mensuration
   • Easy to Medium
   • Video Solution

7. Product M is produced by mixing chemical X and chemical Y in the ratio of 5 : 4. Chemical X is prepared by mixing two raw materials, A and B, in the ratio of 1 : 3. Chemical Y is prepared by mixing raw materials, B and C, in the ratio of 2 : 1. Then the final mixture is prepared by mixing 864 units of product M with water. If the concentration of the raw material B in the final mixture is 50%, how much water had been added to product M?

   1. 328 units
   2. 368 units
   3. 392 units
   4. 616 units
   5. None of the above

   • Correct AnswerChoice (B).
     368 units of water has been added to product M to get the final mixture. Correct answer
   • Explanatory answer
   • Mixtures & Alligation
   • Medium to Hard
   • Video Explanation

8. Find the equation of the graph shown below.
   
   

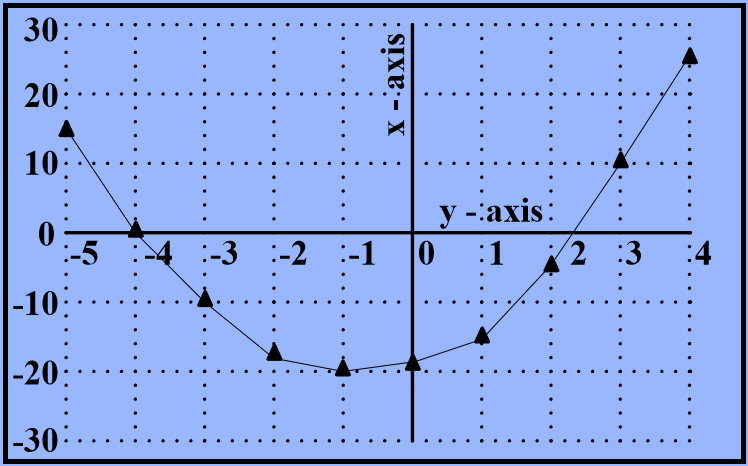
   1. y = 3x - 4
   2. y = 2x² - 40
   3. x = 2y² - 40
   4. y = 2x² + 3x - 19
   5. x = 2y² + 3y - 19

   • Correct AnswerChoice E.
     The equation of the given curve is x = 2y² + 3y - 19 Correct answer
   • Explanatory answer
   • Quadratic Equations
   • Easy
   • Video Solution

9. Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.

   1. 15 and 30
   2. 15 and 40
   3. 17 and 30
   4. 17 and 40
   5. Multiple solutions are possible

   • Choice DThe lengths of the diagnoals are 17 and 40. Correct answer
   • Explanatory answer
   • Coordinate Geometry
   • Easy
   • Video Explanation

10. In the diagram below, CD = BF = 10 units and ∠CED = ∠BAF = 30^o. What would be the area of triangle AED? (Note: Diagram below may not be drawn to scale.)

    

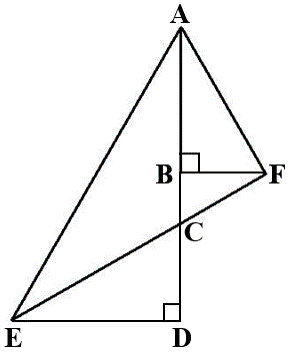
    1. 100 x (\\sqrt{2}\\) + 3)
    2. \\frac{100}{(\sqrt3 + 4)}\\)
    3. \\frac{50}{(\sqrt3 + 4)}\\)
    4. 50 x (\\sqrt{3}\\) + 4)
    5. None of the above

    • Choice DThe area of the triangle is 50(√3 + 4). Correct answer
    • Explanatory answer
    • Geometry
    • Medium
    • Video Solution

11. If f(x² – 1) = x⁴ – 7x² + k₁ and f(x³ – 2) = x⁶ – 9x³ + k₂ then the value of (k₂ – k₁) is _____

    1. 6
    2. 7
    3. 8
    4. 9
    5. None of the above

    • Choice CThe value of (k₂ – k₁) = 8 Correct answer
    • Explanatory answer
    • Functions
    • Easy
    • Video Explanation

12. In the beginning of the year 2004, a person invests some amount in a bank. In the beginning of 2007, the accumulated interest is Rs. 10,000 and in the beginning of 2010, the accumulated interest becomes Rs. 25,000. The interest rate is compounded annually and the annual interest rate is fixed. The principal amount is:

    1. Rs. 16,000
    2. Rs. 18,000
    3. Rs. 20,000
    4. Rs. 25,000
    5. None of the above

    • Choice CThe principal invested is Rs.20,000 Correct answer
    • Explanatory answer
    • Compound Interest
    • Medium
    • Video Solution

13. The taxes for various income slabs are given below:

    Income Slab (I)	Tax rate
    I ≤ 500	0
    500 < I ≤ 2000	5%
    2000 < I ≤ 5000	10%
    5000 < I < 10,000	15%

    There are 15 persons working in an organization. Out of them 3 to 5 persons are falling in each of the income slabs mentioned above. Which of the following is the correct tax range of the 15 person? (e.g., If one is earning Rs. 2000, the tax should be : 500 * 0 + 1500 * 0.05)

    1. 1350 to 7350, both excluded
    2. 1350 to 9800, both included
    3. 2175 to 7350, both excluded
    4. 2175 to 9800, both included
    5. None of the above

    • Choice (A)1350 to 7350, both excluded Correct answer
    • Explanatory answer
    • Percentage
    • Hard
    • Video Explanation

14. If a, b, c and d are four different positive integers selected from 1 to 25, then the highest possible value of \\frac{(a + b) + (c + d)}{(a + b) + (c - d)}\\) would be:

    1. 47
    2. 49
    3. 51
    4. 96
    5. None of the above

    • Correct AnswerChoice (C). The maximum value for the expression is 51. Correct answer
    • Explanatory answer
    • Number Properties
    • Medium
    • Video Solution

XAT TANCET Practice Questions - Listed Topic wise